Repairing Man-Made Meshes via Visual Driven Global Optimization with Minimum Intrusion

Repairing Man-Made Meshes via Visual Driven Global Optimization with Minimum Intrusion

Chu Lei^1,2, Hao Pan², Yang Liu², Wenping Wang¹

¹The University of Hong Kong, ²Microsoft Research Asia

ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2019)

Meshes from ModelNet [Wu et al. 2015] and ShapeNet [Chang et al. 2015] are repaired by our tool that produces large coherent manifold meshes preserving the input visual appearances and features. Each manifold surface patch is colored differently. From top to bottom: the input meshes with scattered and redundant patches, our results with meaningful components and the more concise results when hidden patches are removed (Sec. 6.2). The shell of the car model is rendered in transparency to show inner structures.

Abstract

3D mesh models created by human users and shared through online platforms and datasets flourish recently. While the creators generally have spent large efforts in modeling the visually appealing shapes with both large scale structures and intricate details, a majority of the meshes are unfortunately flawed in terms of having duplicate faces, mis-oriented regions, disconnected patches, etc. , due to multiple factors involving both human errors and software inconsistencies. All these artifacts have severely limited the possible low-level and high-level processing tasks that can be applied to the rich datasets. In this work, we present a novel approach to fix these man-made meshes such that the outputs are guaranteed to be oriented manifold meshes that preserve the original structures, big and small, as much as possible. Our key observation is that the models all visually look meaningful, which leads to our strategy of repairing the flaws while always preserving the visual quality. We apply local refinements and removals only where necessary to achieve minimal intrusion of the original meshes, and global adjustments through robust optimization to ensure the outputs are valid manifold meshes with optimal connections. We test the approach on large-scale 3D datasets, and obtain quality meshes that are more readily usable for further geometry processing tasks.

Paper [PDF]

Code and data [Link]

Supplemental doc [ZIP]

Citation
Lei Chu, Hao Pan, Yang Liu, and Wenping Wang. 2019. Repairing Man-Made Meshes via Visual Driven Global Optimization with Minimum Intrusion. ACM Trans. Graph. 38, 6, Article 158 (November 2019), 18 pages. https://doi.org/10.1145/3355089.3356507
(bibtex)

Algorithm pipeline

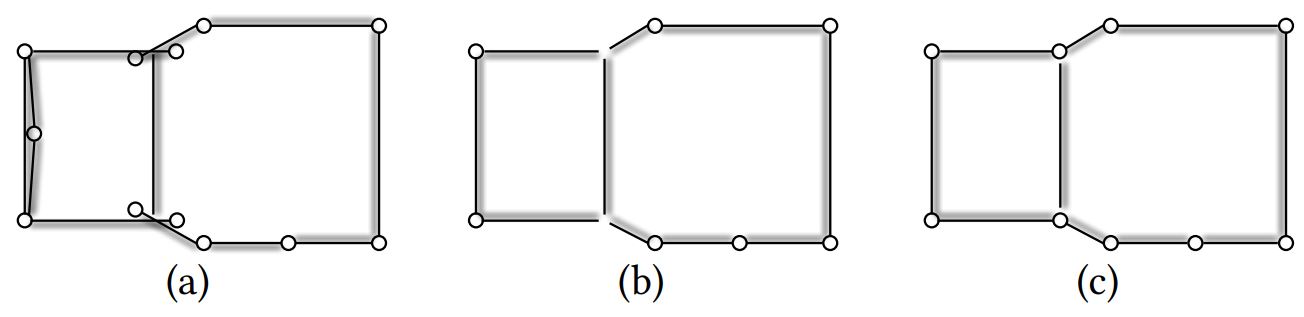2D illustration of the repair pipeline. (a) depicts the input mesh whose faces are shown as line segments, with shadow showing backside of a face. The input mesh has flipped faces, redundant faces and self intersections. (b) shows the cleaned and reoriented face patches after the visual processing step (Sec. 4). (c) shows how the patches are further connected into large and coherent pieces by the manifold mesh reconstruction step (Sec. 5).

The visual driven global mesh repair pipeline applied on a bag model from ShapeNet. From left to right: (a) the input mesh, with its scattered manifold surface patches (Sec. 4.1) rendered in different colors; (b) after preprocessing that merges coinciding vertices and removes duplicate faces (Sec. 3); (c) after visual-driven processing (Sec. 4) that further reorients and merges scattered patches and removes visually redundant patches shown in (c̄); (d) after the global optimization of patch orientation and connection (Sec. 5), intersecting patches (e.g. around the rings) are connected into coherent and larger pieces; (e) the global optimization applied on the subset of patches excluding hidden ones shown in (ē), to enable more connections of different components (Sec. 6.2); (f) is (e) rendered with textures copied from the initial input, which are well preserved by our minimally intrusive approach. The number of manifold surface patches PN is shown for each mesh. For (a) and (b), we have used two-sided shading so that their many flipped faces can be shown.

Results

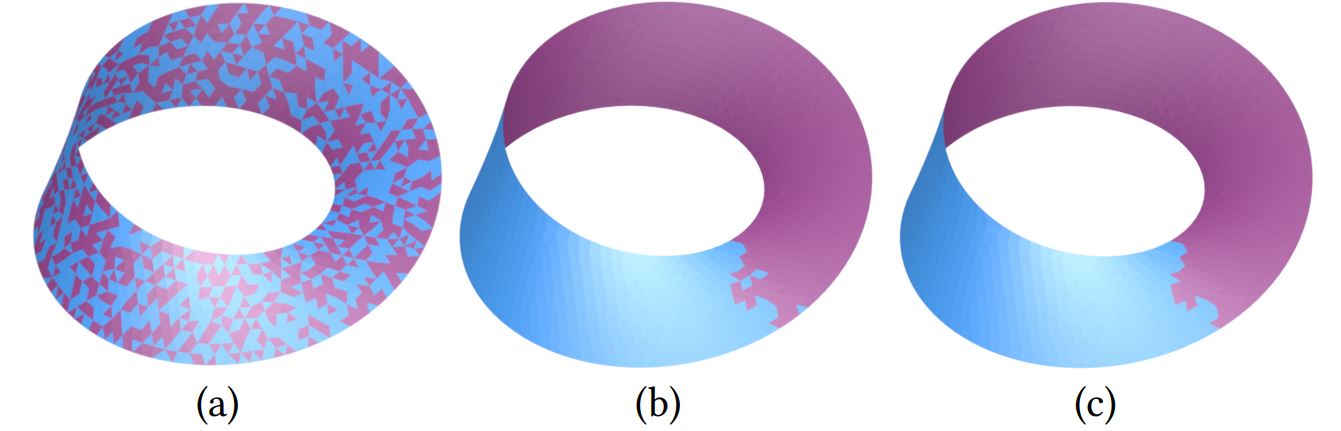An unorientable Möbius strip. From left to right: (a) the input Möbius strip with faces randomly flipped (front in blue, back in purple), (b) result after visual processing that tries to reorient the faces into larger patches with coherent orientations, and (c) result after global manifold mesh reconstruction which further flips certain small patches to obtain a single oriented surface with a boundary curve separating the opposite facing triangles.

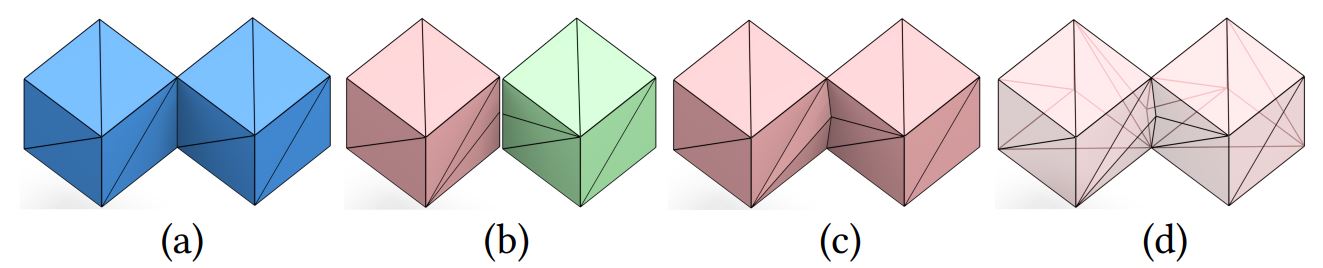Double cubes touching at a common edge, as shown in (a). Under our energy formulation, there are two equally optimal manifold solutions, (b) and (c). We slightly translated the two separate cubes in (b), and perturbed the geometrically coinciding vertices in (c) to better visualize the topology. (d) is a transparent rendering of (c) to show the connections clearly. Note that the one-edge singular curve in (a) is split by our post-processing (Sec. 6.1).

More results by processing ModelNet and ShapeNet datasets. The left side shows results without hidden patch removal, and the right side more concise models with hidden patch removal.

Sample applications

Remeshing on the repaired models. For each pair, the left is the input model, and the right is our fixed model with each patch further remeshed by local operations like edge flipping and vertex smoothing [Fu et al. 2014]. Hidden patches are not removed here. Note that sharp curves on the input models are detected as feature lines and well preserved by remeshing.

Texturing the repaired meshes. Top row shows the repaired meshes that have large manifold components with all sorts of delicate structures preserved. Bottom row are the rendered meshes with textures copied from input meshes. Note how the textures are well transferred. The left two meshes are results with hidden pieces removed, and the right one without.

Solver comparison

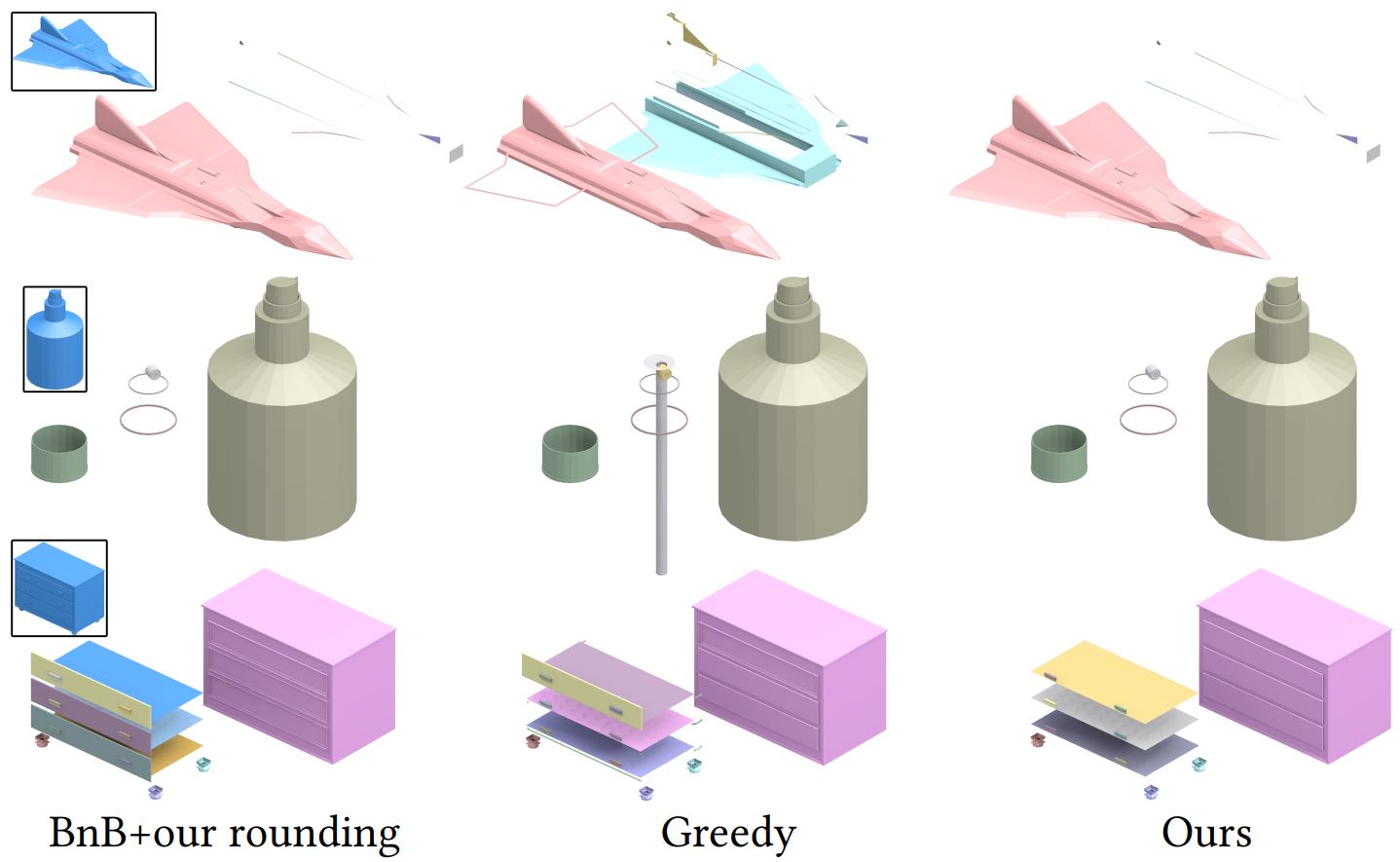Result manifold components by different solvers without hidden patch removal. The input of each test case is shown at upper left corner. The components are rearranged manually to better show the structures. Both BnB and our results are structurally regular and similar, while greedy solver results are more scattered.