Unsupervised Shape Completion via Deep Prior in the Neural Tangent Kernel Perspective

Unsupervised Shape Completion via Deep Prior in the Neural Tangent Kernel Perspective

¹The University of Hong Kong, ²Microsoft Research Asia, ³Texas A&M University

ACM Transactions on Graphics

Completing partial scans of 3D shapes from different categories with large missing areas, by self-supervised training of sparse 3D CNNs that fit to the partial scans without using extra data set. Each example shows the partial scan (left) and the completed model (right).

Abstract

We present a novel approach for completing and reconstructing 3D shapes from incomplete scanned data by using deep neural networks. Rather than being trained on supervised completion tasks and applied on a testing shape, the network is optimized from scratch on the single testing shape, to fully adapt to the shape and complete the missing data using contextual guidance from the known regions. The ability to complete missing data by an untrained neural network is usually referred to as the deep prior. In this paper, we interpret the deep prior from a neural tangent kernel (NTK) perspective and show that the completed shape patches by the trained CNN are naturally similar to existing patches, as they are proximate in the kernel feature space induced by NTK. The interpretation allows us to design more efficient network structures and learning mechanisms for the shape completion and reconstruction task. Being more aware of structural regularities than both traditional and other unsupervised learning-based reconstruction methods, our approach completes large missing regions with plausible shapes and complements supervised learning-based methods that use database priors by requiring no extra training data set and showing flexible adaptation to a particular shape instance.

Paper [arXiv]

Code and data [Link]

Supplemental doc [PDF]

Citation
Lei Chu, Hao Pan, and Wenping Wang. 2021. Unsupervised Shape Completion via Deep Prior in the Neural Tangent Kernel Perspective. ACM Trans. Graph. 40, 3, Article 32
(bibtex)

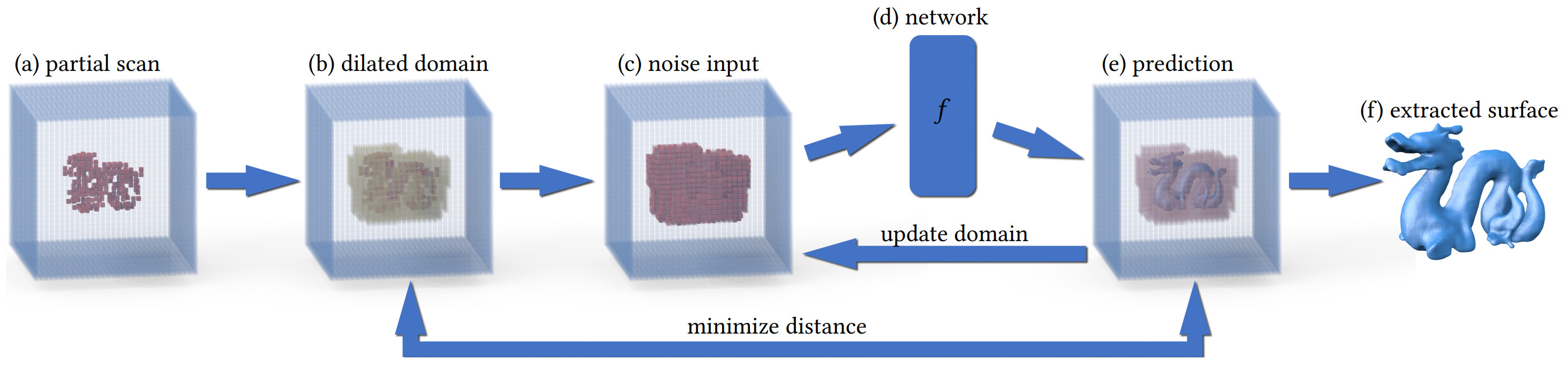
Algorithm pipeline

Illustration of the pipeline. Given an incomplete shape in the form of truncated signed distance function (TSDF) (a), we build a dilated sparse volume with initial regions to be completed (b), and fill the sparsity pattern with noise (c) which is then fed to a 3D sparse encoder/decoder CNN (d) to recover a shape (e). The network is optimized to minimize the differences between (e) and (b) for the known shape regions only. The generation domain is updated gradually during the optimization iterations, to maintain the sparsity of the TSDF volume while also ensuring coverage of the missing regions. After sufficient iterations, we obtain the completed shape (f) extracted from the optimized TSDF.

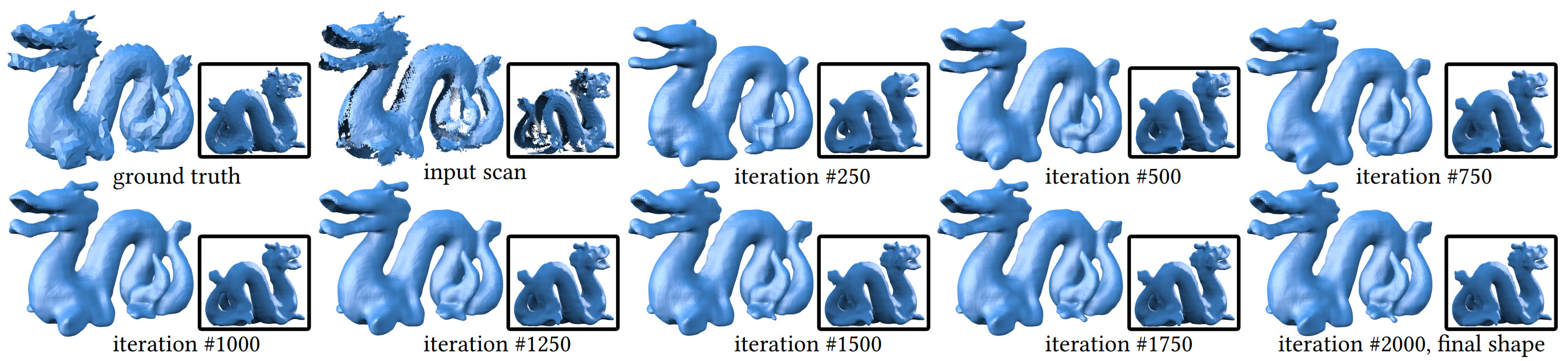The evolution of predicted shapes by optimizing the 3D sparse CNN with stochastic gradient descent to fit to the incomplete input shape, where both the known shape and the unknown regions are gradually recovered.

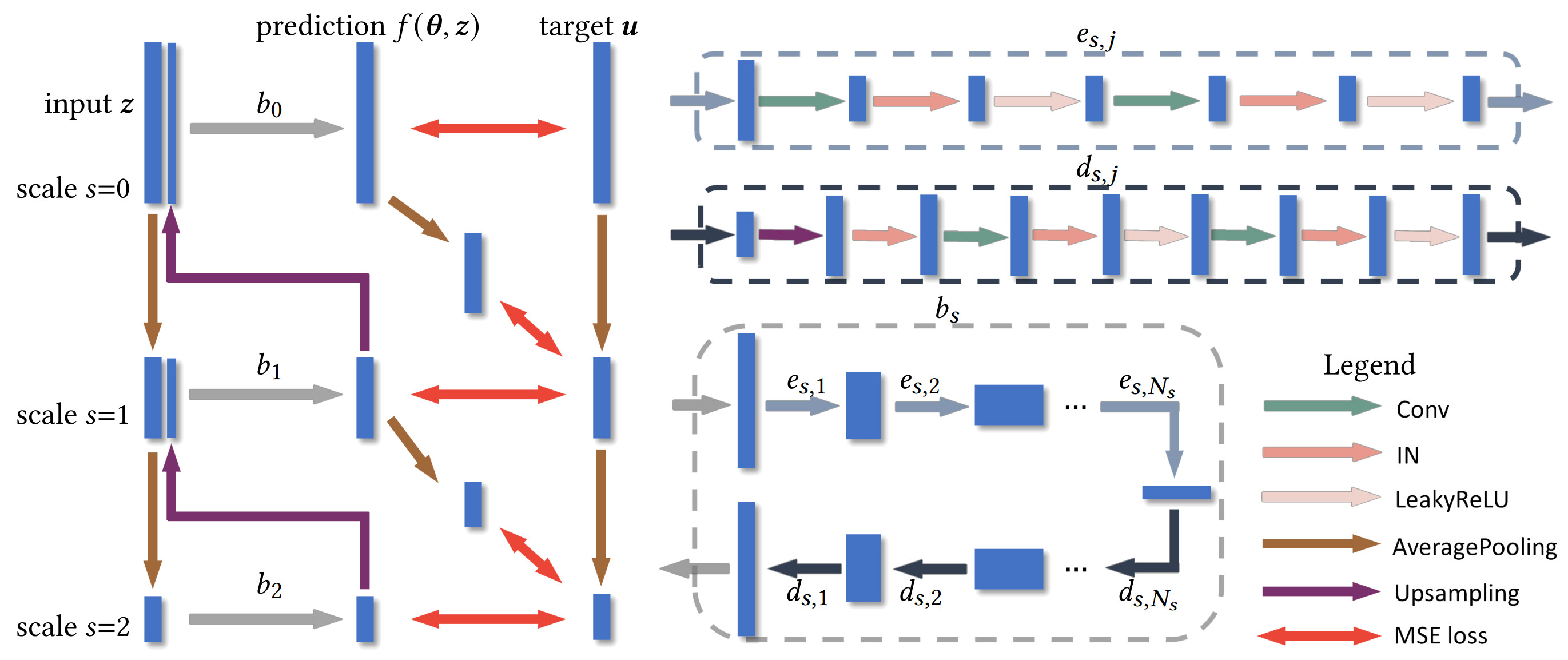The three-scale network structure. Each scale \(s\) uses the downsampled noise vector \(z\downarrow_s\) as input and the downsampled target TSDF \(u\downarrow_s\) as supervision, mapped through the base block network \(b_s\) that is a symmetric pair of encoder [\(e_{s,j}\)] and decoder [\(d_{s,j}\)] without skip connections. \(e_{s,j}\) contains a convolution with stride 2 for downsampling followed by another convolution. \(d_{s,j}\) contains nearest neighbor upsampling followed by two convolutions. All convolutions are followed by instance normalization and leaky ReLU activation.

NTK Analysis

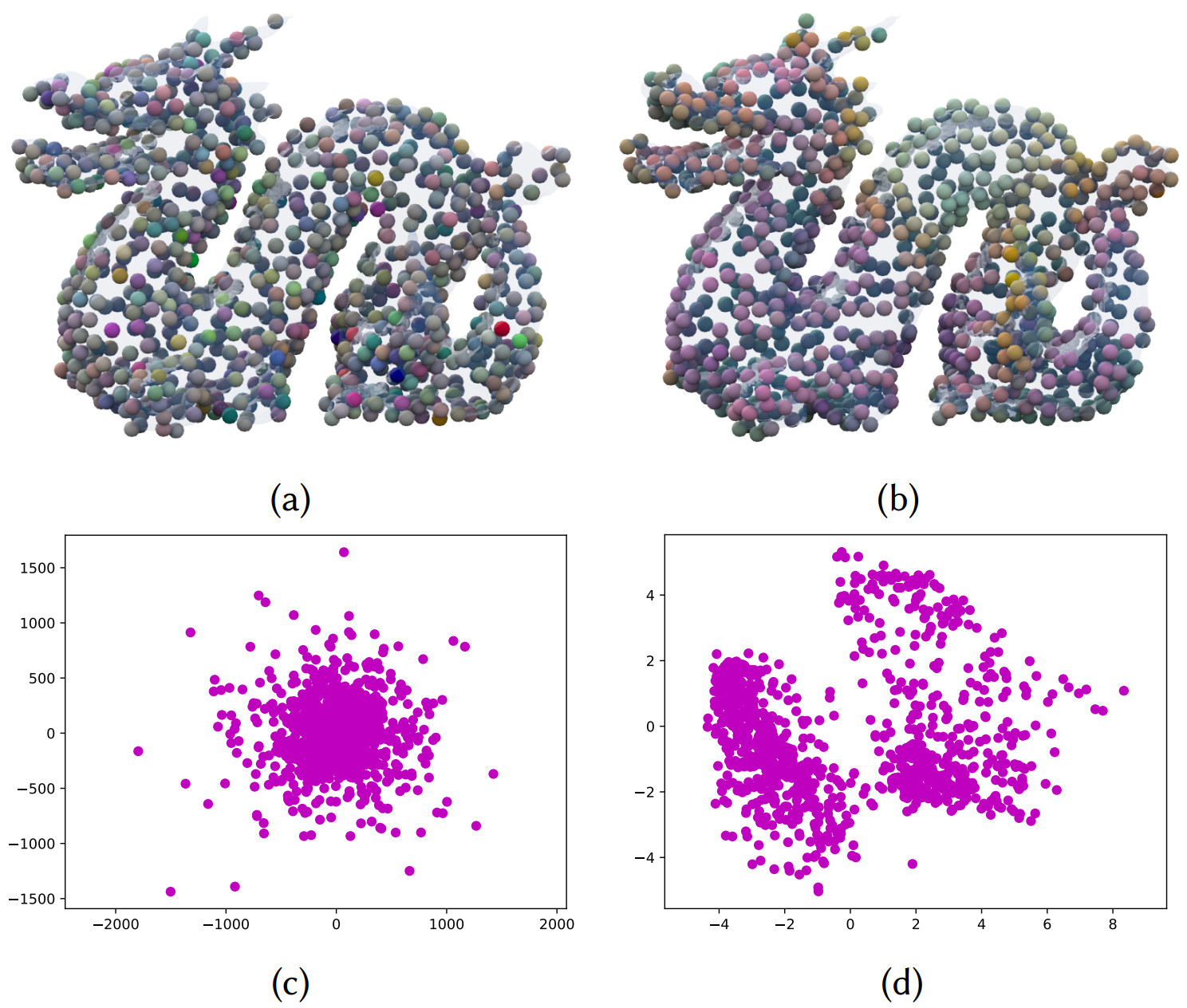Kernel PCA analysis with the NTK, before (left) and after (right) network training. The top three principal component coordinates are used for color coding the spatial points in (a),(b), and the top two principal component coordinates used for 2D plots in (c),(d). Before training, the points are embedded randomly in NTK, but regular patterns emerge with self similarities after training.

Results

More results of shape completion by our unsupervised method. The diverse objects have been collected from ShapeNet, Thingi10k and Free3D, with challenging features like slim bars, thin layers and large missing regions. Our method plausibly recovers the features by automatically exploiting the self-similarities and overall coherence with known parts.

Ablation Study

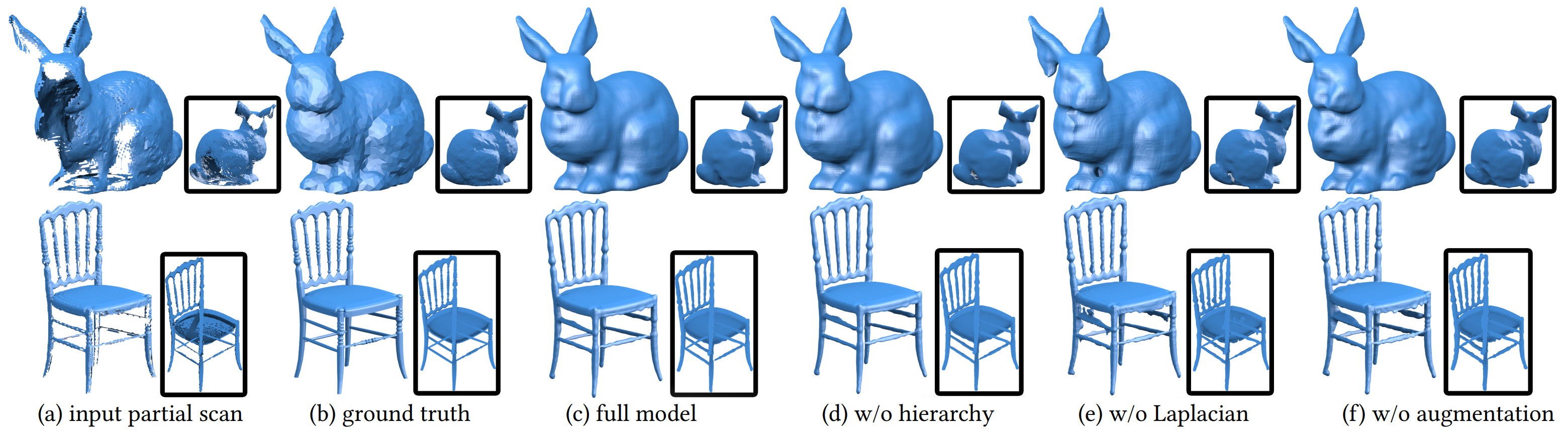Ablation test results on two examples. (c) the full model result is close to the ground truth despite the large missing regions. (d) without multi-scale hierarchy, holes appear at the bunny tail due to difficulty for bridging the large gaps there. (e) without Laplacian smoothness, local regularity is lost and extraneous parts emerge. (f) without augmentation, the completed shapes are less fit and plausible.

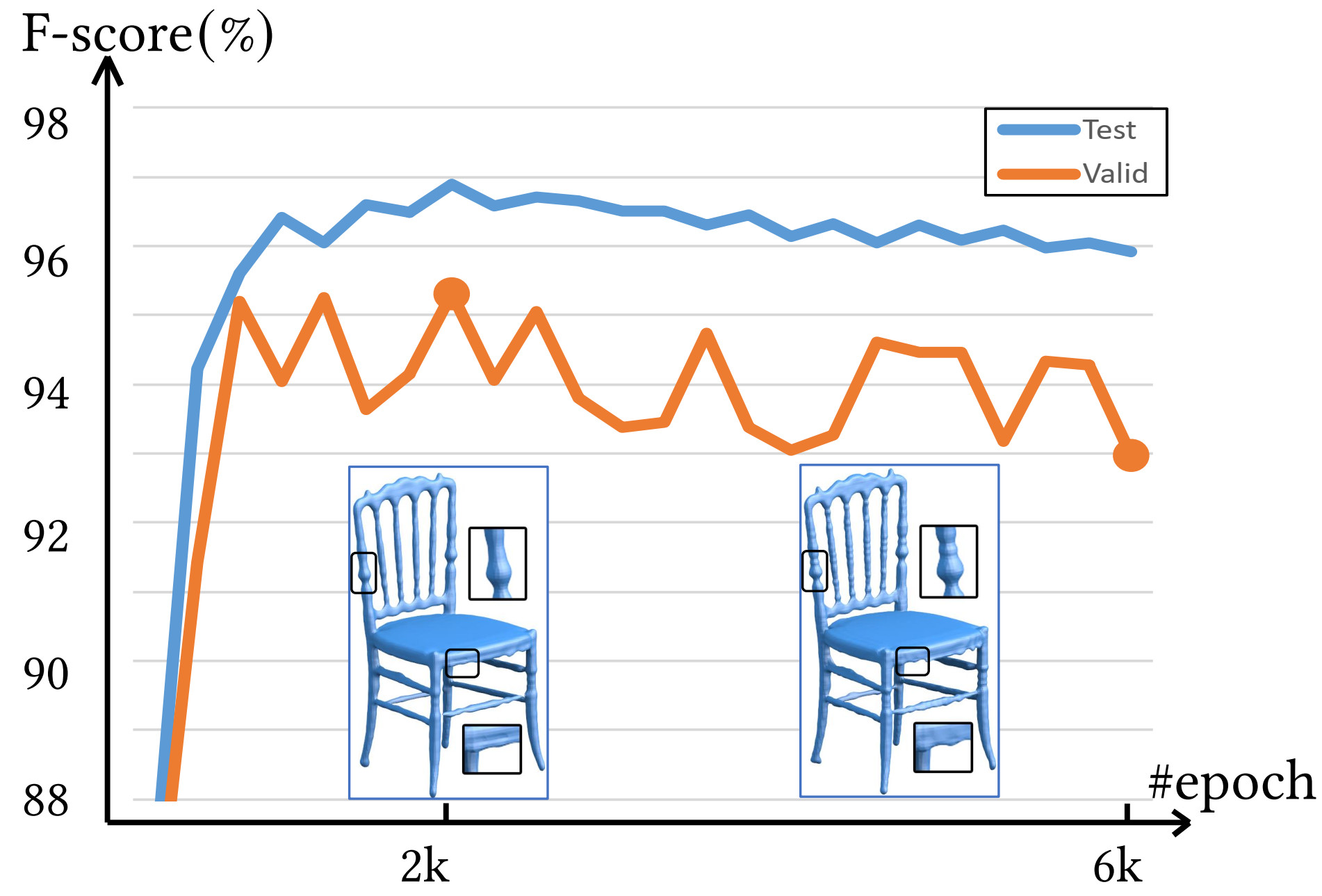The average F-score with respect to the number of training epochs, evaluated on 10 validation models and 20 test models, respectively. The shapes quickly recover during the early epochs, reach stable around 2k, but then slowly degrade by fitting to the extra details with more epochs. This demonstrates the necessity of early stopping.

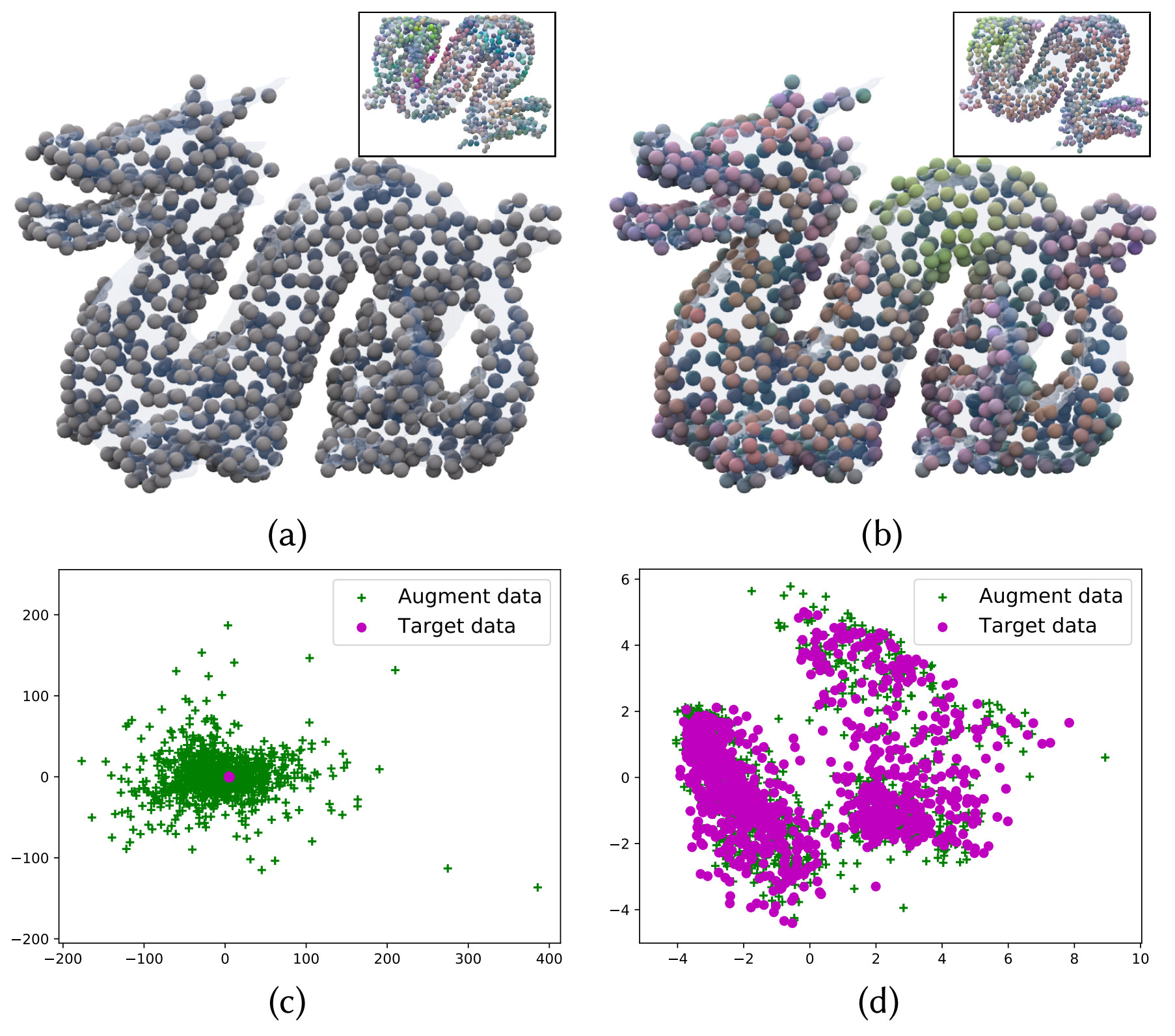Kernel PCA analysis with NTK for 2k sample points, half from the target models (a),(b) and half from the augmented models (upper right corners of (a),(b)), trained without (left) and with augmentation (right). The scatter plot and color coding are in the same format as above. Without augmentation, the two point sets show no correlation under NTK; with augmentation, the two sets have strong correlations.